| |
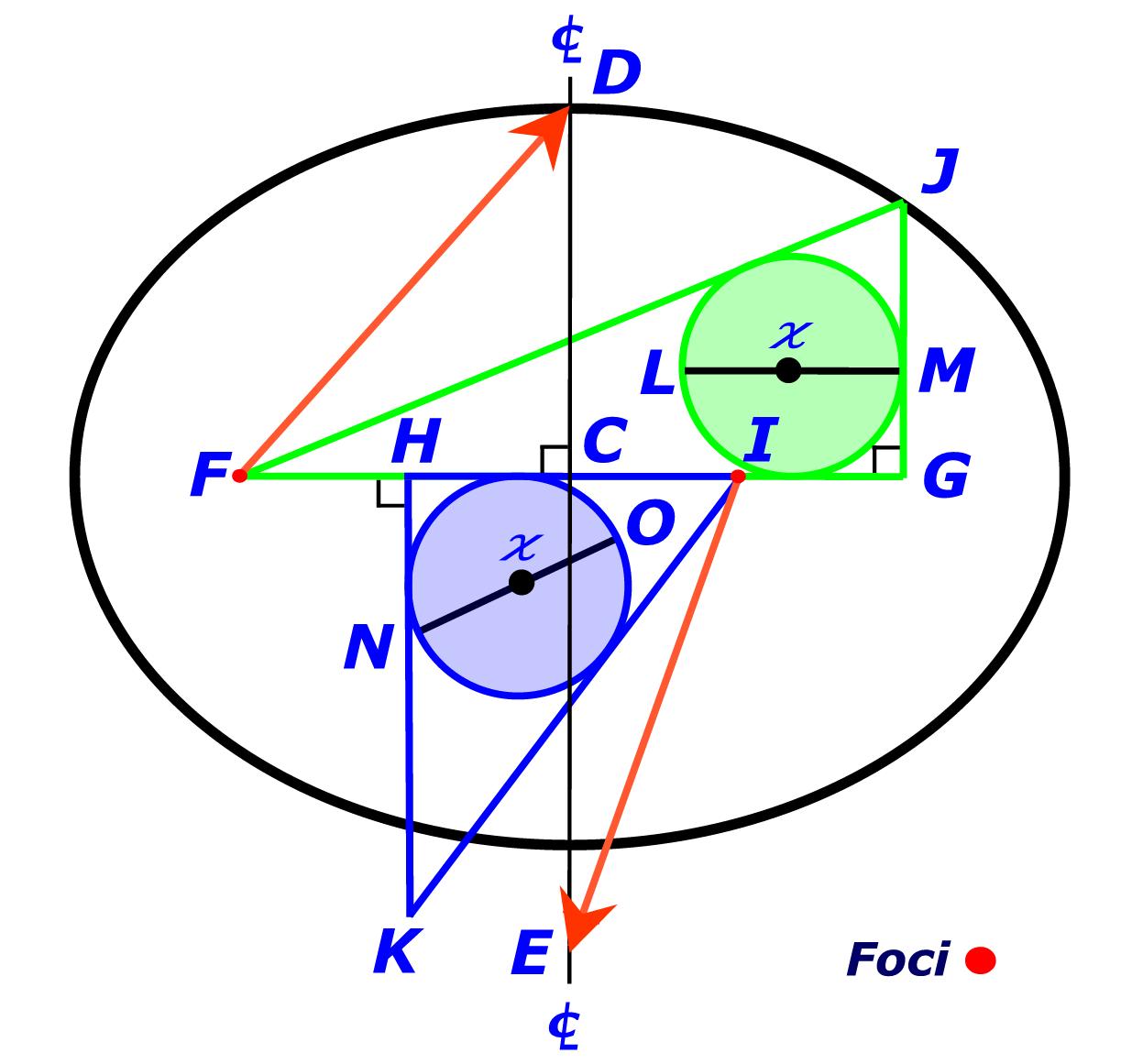
With Points F and G as Foci,
draw an ellipse
through Point D.
Point J is on the
ellipse, which
is referred to as a radius
ellipse.
|
|
| |
Extend the Center Line
as required
Draw a Vector Line EI
that is equal
to Line GH
from Point I
to the Center Line.
Draw a Vector Line DF
that is equal
to Line FI
from Point F to the Center Line. |
|
 |
|
 |
| |
Transpose Pythagorean Triangles
FGJ and
HIK as indicated.
Extend the Center Line
as required. |
|
|
Inscribe Circles (in-circles)
FGJ and HIK
with centers at

and
respective diameters LM and NO.
Bisect Lines FG and HI
with Center Lines. |
|
| |
Construct a paired
Pythagorean Triangle FGJ
in accordance with base, side, and
hypotenuse as indicated in the
below Table of Formulas.
A pair of Pythagorean Triangles
have short sides,
radius (r) and base (b),
which vary by
the Elliptical Constant (EC) =
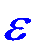 . . |
|
| |
Construct a Pythagorean Triangle
HIK
in accordance with base, side, and
hypotenuse as indicated in the
below Table of Formulas.
Pythagorean Triangles are triangles
with
a right angle; and,
all sides that are integers. |
|
| |
Pulsoid Theorem (PTm) |
V |
= |
|
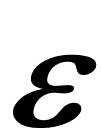 P2 P2 |
|
|
|
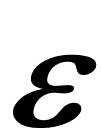 |
|
= |
Elliptical
Constant (EC) |
= |
|
One |
|
x |
|
= |
Integer
(base 10)=b/2 |
|
|
|
| |
All
Vector
Lines
are
equal. |
. |
|
DF & EI |
|
=
|
Vector
(V)=(b/2)2 |
= |
|
x2 |
|
FGJ |
|
= |
Pythagorean
radius
Triangle |
|
FG |
|
=
|
wave
(w)=b2/2–b |
= |
|
2(x2–x) |
|
GJ |
|
=
|
radius
(r)=b– |
= |
|
2x–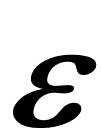 |
|
FJ |
|
=
|
hypotenuse
(h)=b2/2–b+ |
= |
|
2x2–2x+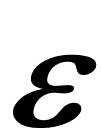 |
|
HIK |
|
= |
Pythagorean
Vector
Triangle |
|
HI |
|
=
|
base
(b), V-wave,
(Vw) |
= |
|
2x |
|
HK |
|
=
|
V-radius
(Vr)=b2/4
– |
= |
|
x2–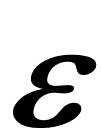 |
|
IK |
|
=
|
V-hypotenuse
(Vh)=b2/4+ |
= |
|
x2+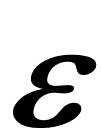 |
|
FGJ |
|
=
|
radius-Resoloid
(in-circle) |
= |
|
rR |
|
LM |
|
= |
r-diameter
(rd)=b–2 |
= |
|
2(x–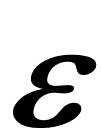 ) ) |
 L L |
|
=
|
r-radius
(rr)=b/2– |
= |
|
x–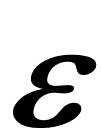 |
|
HIK |
|
=
|
Vector-Resoloid
(in-circle) |
= |
|
VR |
|
NO |
|
=
|
VR-diameter
(VRd)=b–2 |
= |
|
2(x–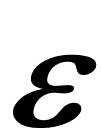 ) ) |
 N N |
|
=
|
VR-radius
(VRr)=b/2– |
= |
|
x– |
The Pythagorean Theorem, a2 + b2
= c2,
is an an incredible coincidence
of
number theory, which arises from
the
Emergent Ellipsoid and
the Natural source of
Mathematics. |
|
A Pythagorean Triangle Pair (PTP)
can be mapped to
every integer greater
than One.
Four angles (two of the six angles are right angles)
and all six sides of a Pythagorean Triangle Pair
are of unlike values. |
The simplest equation
for
the in-diameter of a circle
inscribed within any right triangle is:
|
| |
An in-diameter of a right
triangle
equals side "a" plus side "b"
minus the hypotenuse "c". |
|
|
Amazingly, the diameters
of both circles inscribed within
each
different
Pythagorean Triangle,
of a given pair, are even integers,
that are . . .
identical to one another.
Thus, the radii of the inscribed circles
are also equal integers.
|
|